Find the Equation of a Line, a fundamental concept in algebra, unlocks the secrets of straight lines. Understanding how to derive their equations is crucial for tackling problems in various fields, from physics to economics. This guide delves into different methods for finding the equation of a line, covering everything from basic principles to more complex scenarios like parallel and perpendicular lines.
We’ll explore various forms of linear equations and demonstrate how they can be applied in real-world contexts.
This detailed exploration will walk you through finding the equation of a line given two points, a point and a slope, the y-intercept and slope, or even two parallel or perpendicular lines. Each method will be illustrated with clear examples and practical applications. You’ll also discover the advantages and disadvantages of different forms of linear equations and learn how to convert between them.
Introduction to Linear Equations
A linear equation in two variables describes a straight line on a coordinate plane. It represents a relationship where the change in one variable is consistently related to the change in the other variable. Understanding linear equations is fundamental in mathematics, as they model numerous real-world phenomena, from simple cost-benefit analyses to more complex scientific models. They’re crucial for making predictions and estimations based on observed patterns.Linear equations are equations where the variables are raised to the power of one.
This simplicity makes them easy to visualize and manipulate. The solutions to these equations form a straight line when plotted on a graph. This characteristic allows us to predict future values based on known values and patterns, making them powerful tools in various applications.
Definition of a Linear Equation
A linear equation in two variables, typically x and y, is an equation that can be written in the form Ax + By = C, where A, B, and C are constants, and A and B are not both zero. This form represents a relationship where the variables are directly or inversely proportional to each other.
General Form of a Linear Equation
The general form of a linear equation is Ax + By = C. This form is useful for identifying the coefficients of the variables and the constant term. For example, in the equation 2x + 3y = 6, A = 2, B = 3, and C = 6.
Slope and Y-intercept
The slope of a line, often denoted by the letter ‘m’, represents the rate of change of y with respect to x. A positive slope indicates an upward trend, while a negative slope indicates a downward trend. The y-intercept, denoted by the letter ‘b’, is the point where the line crosses the y-axis. It represents the value of y when x is zero.
These two key components completely define a line’s characteristics and position on a graph. Understanding these components allows for quick graphing and interpretation of the equation’s implications.
Relationship Between Different Forms
Different forms of linear equations represent the same line but emphasize different aspects. The table below illustrates the relationships between slope-intercept form, point-slope form, and standard form.
| Form | Equation | Description |
|---|---|---|
| Slope-intercept form | y = mx + b | y is explicitly defined in terms of x, where ‘m’ is the slope and ‘b’ is the y-intercept. |
| Point-slope form | y – y1 = m(x – x1) | Defines a line using a point (x1, y1) on the line and the slope ‘m’. |
| Standard form | Ax + By = C | A, B, and C are constants. This form is useful for identifying the intercepts and the relationship between the variables. |
Understanding these relationships allows for seamless conversions between different representations, facilitating a more versatile approach to working with linear equations. For example, converting from standard form to slope-intercept form reveals the slope and y-intercept, enabling graphing.
Finding the Equation Given Two Points

Once you understand the fundamental concept of a linear equation, the next crucial step is determining the equation when you’re given two points on the line. This process is essential for various applications, from modeling real-world scenarios to solving geometric problems. This method leverages the point-slope form of a linear equation, which provides a direct pathway to finding the equation when the slope and a point on the line are known.
Calculating the Slope
The slope of a line, often denoted by the letter ‘m’, represents the rate of change between the y-coordinates and the x-coordinates of any two points on the line. To calculate the slope, we use the formula: m = (y 2
-y 1) / (x 2
-x 1). This formula is derived from the concept of rise over run, which directly relates the vertical change (rise) to the horizontal change (run) between points.
Using the Point-Slope Form
The point-slope form of a linear equation is expressed as y – y 1 = m(x – x 1). This formula is particularly useful because it directly incorporates the slope (m) and the coordinates of a point (x 1, y 1) on the line. Substituting these values into the formula immediately yields the equation of the line.
Example: Finding the Equation Through (2, 5) and (4, 9)
Let’s determine the equation of a line passing through the points (2, 5) and (4, 9). First, we calculate the slope:
m = (9 – 5) / (4 – 2) = 4 / 2 = 2
Now, we use the point-slope form, selecting one of the points (let’s use (2, 5)):
y – 5 = 2(x – 2)
Simplifying the equation yields:
y – 5 = 2x – 4
y = 2x + 1
Figuring out the equation of a line can be tricky, but it’s a fundamental math skill. While I’m wrestling with the complexities of linear equations, I also have to say, I’m really digging the new song by dam funk and nite jewel, “can u read me” dam funk and nite jewel share new nite funk song can u read me.
It’s got that cool, jazzy vibe that makes me want to graph some more lines! Hopefully, I can get back to finding those equations soon.
Therefore, the equation of the line passing through (2, 5) and (4, 9) is y = 2x + 1.
Step-by-Step Procedure
| Step | Description | Calculation (using (2, 5) and (4, 9)) |
|---|---|---|
| 1 | Calculate the slope (m). | m = (9 – 5) / (4 – 2) = 4 / 2 = 2 |
| 2 | Choose one of the given points (x1, y1). | (x1, y1) = (2, 5) |
| 3 | Substitute the slope (m) and the point (x1, y1) into the point-slope form: y – y1 = m(x – x1). | y – 5 = 2(x – 2) |
| 4 | Simplify the equation to obtain the slope-intercept form: y = mx + b. | y – 5 = 2x – 4 y = 2x + 1 |
Finding the Equation Given a Point and the Slope
Unlocking the equation of a line becomes straightforward when you know a point on the line and its slope. This method, crucial in various mathematical and real-world applications, relies on the point-slope form of a linear equation. This approach simplifies the process compared to finding the equation from two points, as it leverages the direct relationship between the slope and the coordinates of a known point.Understanding the Point-Slope Form is essential for determining the equation of a line.
The point-slope form is a powerful tool for this task, offering a concise and direct way to represent the equation of a line. It directly connects the slope and a point on the line, making it a practical method for various applications.
Point-Slope Form of a Line
The point-slope form of a linear equation is expressed as y – y 1 = m(x – x 1), where ‘m’ represents the slope, and (x 1, y 1) represents a point on the line. This formula is fundamental to deriving the equation when a slope and a point are known.
Examples and Calculations, Find the Equation of a Line
Let’s illustrate the process with a few examples:
-
Finding the equation of a line with a slope of 2 and passing through the point (3, 5).
Substituting m = 2, x 1 = 3, and y 1 = 5 into the point-slope form:y – 5 = 2(x – 3)
Simplifying this equation, we get:
y – 5 = 2x – 6
y = 2x – 1
-
Consider a line with a slope of -1/2 and passing through the point (-2, 4).
Using the point-slope form:y – 4 = -1/2(x – (-2))
Simplifying:
y – 4 = -1/2(x + 2)
y – 4 = -1/2x – 1
y = -1/2x + 3
-
If a line has a slope of 0 and passes through the point (1, -3),
The point-slope form becomes:y – (-3) = 0(x – 1)
y + 3 = 0
y = -3
This example demonstrates a horizontal line.
Comparison Table
| Slope (m) | Point (x1, y1) | Equation of the Line |
|---|---|---|
| 2 | (3, 5) | y = 2x – 1 |
| -1/2 | (-2, 4) | y = -1/2x + 3 |
| 0 | (1, -3) | y = -3 |
This table clearly demonstrates the diverse equations that can result from different combinations of slopes and points. The examples show how the point-slope form is used to derive the equation of a line in each case.
Finding the Equation Given the Y-intercept and the Slope
Unlocking the equation of a line becomes straightforward when armed with its y-intercept and slope. This method relies on the slope-intercept form of a linear equation, a fundamental tool in algebra and various real-world applications. Knowing the y-intercept and slope allows us to immediately determine the line’s equation without the need for additional points.
Understanding the Slope-Intercept Form
The slope-intercept form of a linear equation is expressed as y = mx + b, where ‘m’ represents the slope and ‘b’ represents the y-intercept. This form directly connects the steepness of the line (slope) with its vertical position (y-intercept) on the coordinate plane. The slope indicates the rate of change of ‘y’ with respect to ‘x’, while the y-intercept is the point where the line crosses the y-axis.
Applying the Method
To find the equation of a line given the y-intercept and slope, simply substitute the known values of ‘m’ and ‘b’ into the slope-intercept form (y = mx + b). This yields the equation of the line.
Examples
Let’s illustrate this with some examples:
- Example 1: If the y-intercept is 3 and the slope is 2, the equation of the line is y = 2x + 3. This line passes through the point (0, 3) and has a constant upward inclination of 2 units for every 1 unit increase in x.
- Example 2: If the y-intercept is -5 and the slope is -1, the equation of the line is y = -1x – 5. This line passes through the point (0, -5) and has a downward inclination of 1 unit for every 1 unit increase in x.
- Example 3: If the y-intercept is 7 and the slope is 0.5, the equation of the line is y = 0.5x + 7. This line passes through the point (0, 7) and has a gradual upward inclination.
Table of Equations
The following table demonstrates various line equations based on different y-intercepts and slopes.
| Y-intercept (b) | Slope (m) | Equation of the Line |
|---|---|---|
| 5 | 2 | y = 2x + 5 |
| -2 | -1 | y = -1x – 2 |
| 0 | 3 | y = 3x |
| 10 | 0.5 | y = 0.5x + 10 |
| -7 | 4 | y = 4x – 7 |
Finding the Equation Given Two Parallel Lines
Parallel lines are lines in a plane that never intersect. A fundamental property of parallel lines is their slopes. Understanding this relationship is crucial for determining the equation of a line parallel to a given line. This section delves into the specifics of finding the equation of a line parallel to a known line, given a point on the new line.Parallel lines have the same slope.
This means that if you know the slope of one parallel line, you know the slope of all other parallel lines. This property simplifies the process of finding the equation of a line parallel to a given line. We’ll explore this relationship and how it allows us to easily find the equation of a new line.
Figuring out the equation of a line can be surprisingly straightforward, especially when you’re dealing with two points. But sometimes, you need a little extra inspiration, like listening to the groovy sounds of Thee Oh Sees drop. Thee Oh Sees drop really gets the creative juices flowing, and that’s a great way to refresh your mind when tackling those tricky slope and y-intercept calculations.
Once you’ve got the equation, you’re ready to graph and master those linear functions!
Relationship Between Parallel Lines and Slopes
Parallel lines in a two-dimensional coordinate system share a unique characteristic: their slopes are equal. This means that if two lines are parallel, the ratio of the change in y to the change in x (rise over run) for both lines will be the same. This shared slope is a defining feature of parallel lines, allowing us to identify and work with them mathematically.
Mathematically, if line 1 and line 2 are parallel, the slope of line 1 (m 1) is equal to the slope of line 2 (m 2). Or m 1 = m 2.
Finding the Equation of a Parallel Line
To find the equation of a line parallel to a given line and passing through a specific point, follow these steps:
- Determine the slope of the given line. This is often the first step. Once you have the slope of the given line, you automatically know the slope of the parallel line.
- Use the point-slope form of a linear equation, which is y – y1 = m(x – x 1). This formula is a key tool for finding the equation of a line when you know its slope and a point on the line. Substitute the known slope (from the parallel line) and the coordinates of the given point (x 1, y 1) into the formula.
- Simplify the equation to the slope-intercept form, which is y = mx + b. This is the standard form for representing a linear equation.
Example
Find the equation of the line that is parallel to the line 2x + y = 5 and passes through the point (2, 3).
- First, find the slope of the given line. Rearrange the equation 2x + y = 5 into slope-intercept form (y = mx + b): y = -2x + 5. The slope of this line is -2.
- Since the parallel line has the same slope, the slope of the new line is also –
Now, use the point-slope form: y – 3 = -2(x – 2).
- Simplify the equation to slope-intercept form: y – 3 = -2x + 4. Thus, y = -2x + 7.
This example demonstrates how to find the equation of a line parallel to a given line through a specific point. The resulting equation represents the parallel line.
Finding the Equation Given Two Perpendicular Lines
Perpendicular lines are lines that intersect at a 90-degree angle. Understanding the relationship between their slopes is crucial for finding the equation of one line given the other and a point. This knowledge is fundamental in various geometric and algebraic applications, from constructing precise shapes to calculating distances and orientations.The key to finding the equation of a perpendicular line lies in recognizing the inverse negative relationship between their slopes.
This unique property allows us to determine the slope of the perpendicular line if we know the slope of the given line.
Relationship Between Slopes of Perpendicular Lines
The slopes of two perpendicular lines are negative reciprocals of each other. This means if the slope of one line is ‘m’, the slope of the perpendicular line is ‘-1/m’. This relationship arises from the properties of right-angled triangles formed by the lines and their intercepts. A change in the x-coordinate on one line will have a corresponding, inversely proportional change in the y-coordinate on the other.
Finding the Equation of a Perpendicular Line
To find the equation of a line perpendicular to a given line passing through a specific point, follow these steps:
- Determine the slope of the given line. If the equation of the given line is in the form y = mx + b, the slope is ‘m’. If the equation is not in this form, rearrange it to isolate ‘y’ to find the slope.
- Calculate the slope of the perpendicular line. The slope of the perpendicular line is the negative reciprocal of the given line’s slope. If the given slope is ‘m’, the perpendicular slope is ‘-1/m’.
- Use the point-slope form of a linear equation. The point-slope form is y – y 1 = m(x – x 1), where (x 1, y 1) is the given point and ‘m’ is the slope of the perpendicular line. Substitute the coordinates of the given point and the calculated perpendicular slope into this formula.
- Simplify the equation. Distribute the slope to the terms inside the parentheses and isolate ‘y’ to get the equation in the form y = mx + b.
Example
Find the equation of the line perpendicular to the line y = 2x + 3 and passing through the point (4, 1).
- The given line has a slope of 2. Therefore, the slope of the perpendicular line is -1/2.
- Using the point-slope form with the point (4, 1) and slope -1/2, we get: y – 1 = -1/2(x – 4).
- Simplifying the equation gives: y – 1 = -1/2x + 2. Adding 1 to both sides, we get y = -1/2x + 3.
The equation of the line perpendicular to y = 2x + 3 and passing through (4, 1) is y = -1/2x + 3.
Applications of Linear Equations
Linear equations, seemingly simple mathematical expressions, play a surprisingly crucial role in various real-world scenarios. Their ability to model relationships between variables makes them invaluable tools across diverse fields. From predicting future trends to analyzing physical phenomena, linear equations provide a powerful framework for understanding and interpreting data.
Real-World Scenarios
Linear equations are fundamental to modeling relationships where the rate of change is constant. This constant rate of change is a defining characteristic of many natural and human-made systems. Consider a scenario where a car travels at a steady speed. The distance covered by the car is directly proportional to the time spent traveling, and this relationship can be expressed as a linear equation.
Similarly, the cost of producing items often increases linearly with the number of items produced.
Importance in Physics
In physics, linear equations are used extensively to describe various phenomena. The motion of an object with constant velocity is a prime example. The relationship between position, time, and velocity is precisely represented by a linear equation. For instance, if a train travels at a constant speed of 60 km/hr, the distance it covers after ‘t’ hours can be calculated using the linear equation distance = 60t.
Furthermore, relationships involving forces, such as Hooke’s Law, often involve linear equations.
Importance in Economics
In economics, linear equations are instrumental in modeling supply and demand curves. The relationship between price and quantity demanded or supplied is often approximately linear. This allows economists to predict how changes in price affect market equilibrium. Linear equations also underpin cost functions, which show how the cost of production varies with the level of output. A company’s total cost might be a linear function of the number of items produced, where the slope represents the variable cost per item.
Applications in Other Fields
Linear equations are applicable beyond physics and economics. In finance, they are used to calculate simple interest or to project future investments. In engineering, they are employed to design structures and systems. In everyday life, linear equations are used to determine the amount of ingredients needed for a recipe or to calculate the time needed to complete a task.
Finding the equation of a line can be tricky, but it’s a fundamental math skill. Learning how to use reactions in Discord on Android, like a thumbs up or a heart, might seem unrelated, but both involve understanding the relationships between different elements. Knowing how to use reactions in Discord on Android, as shown in this helpful guide, can improve communication efficiency.
Ultimately, both topics are about understanding how different variables interact to achieve a desired outcome, just like finding the equation of a line.
Illustrative Examples
- Calculating the Cost of Materials: A construction company charges $50 per square meter of roofing material, plus a fixed installation fee of $200. The total cost (C) for ‘x’ square meters of roofing is represented by the linear equation C = 50x + 200. If the company needs to cover 10 square meters, the total cost would be $700.
- Predicting Sales: A company’s sales have been increasing at a steady rate of $1000 per month. If the current sales are $5000, the linear equation for future sales (S) in ‘t’ months is S = 1000t + 5000. To predict sales after 6 months, substitute t = 6 into the equation to find S = 11000.
Summary Table
| Application Area | Scenario | Linear Equation Example |
|---|---|---|
| Construction | Calculating material costs | C = 50x + 200 |
| Sales Forecasting | Predicting monthly sales | S = 1000t + 5000 |
| Physics (Motion) | Calculating distance traveled at constant speed | d = vt |
| Economics (Supply/Demand) | Modeling the relationship between price and quantity | Q = mP + c |
Different Forms of Linear Equations: Find The Equation Of A Line
Welcome back to the linear equation exploration! We’ve covered various methods for finding the equation of a line, but now let’s delve into the different forms these equations can take. Understanding these forms is crucial for choosing the most efficient approach for a given problem and for interpreting the characteristics of a line.Different forms of linear equations offer different perspectives on the same relationship between variables.
Each form emphasizes specific aspects of the line, making certain calculations easier and providing different insights. We’ll explore the strengths and weaknesses of each representation.
Slope-Intercept Form
The slope-intercept form, y = mx + b, is arguably the most common and useful form for understanding a line’s behavior. It immediately reveals the slope (m) and the y-intercept (b). The slope, often denoted by ‘m’, indicates the steepness and direction of the line. The y-intercept, represented by ‘b’, is the point where the line crosses the y-axis.
This form is highly advantageous for graphing a line, as the y-intercept provides a starting point and the slope dictates how to extend the line. However, if the equation is not readily given in this form, finding the slope and y-intercept might require additional calculations.
Point-Slope Form
The point-slope form, y – y 1 = m(x – x 1), is invaluable when you know the slope of a line and a point on the line. This form allows you to directly write the equation without first needing the y-intercept. This form is especially practical when working with lines whose y-intercept is not immediately apparent or when you have a point and the slope.
Its downside is that it’s not as readily interpretable for visualizing the line on a graph.
Standard Form
The standard form, Ax + By = C, is useful for representing lines that have integer coefficients and are particularly well-suited for finding the x- and y-intercepts directly. This form, where A, B, and C are integers, often makes it easier to determine the intercepts (the points where the line crosses the axes). A key disadvantage is that it’s not as easily related to the line’s slope and its inclination.
Conversion Between Forms
Converting between forms is a valuable skill. To convert from slope-intercept form to point-slope form, simply identify the slope and a point on the line. To convert from point-slope form to slope-intercept form, distribute the slope and solve for ‘y’. To convert from slope-intercept form to standard form, rearrange the equation to match the standard form Ax + By = C.
To convert from standard form to slope-intercept form, solve for ‘y’. Each conversion process involves manipulating the equation to isolate the variables in the desired format.
Comparison Table
| Form | Equation | Advantages | Disadvantages |
|---|---|---|---|
| Slope-Intercept | y = mx + b | Easy to graph, readily shows slope and y-intercept. | Requires slope and y-intercept. |
| Point-Slope | y – y1 = m(x – x1) | Useful with known slope and point, avoids y-intercept calculation. | Not as visually intuitive as slope-intercept. |
| Standard Form | Ax + By = C | Easy to find intercepts, often integer coefficients. | Not easily related to slope. |
Special Cases of Linear Equations
Linear equations, while seemingly simple, can exhibit special characteristics. Understanding these special cases, such as horizontal and vertical lines, is crucial for a complete grasp of their properties and applications. These exceptions to the typical slope-intercept form provide unique insights into how different relationships between variables can be represented graphically.
Horizontal Lines
Horizontal lines are characterized by a constant y-value for all x-values. This constant y-value is the y-intercept of the line. Consequently, the slope of a horizontal line is always zero.
The equation of a horizontal line is y = b, where b is the y-intercept.
For example, the line y = 3 is a horizontal line passing through the point (0, 3). Similarly, y = -2 is a horizontal line passing through the point (0, -2).To find the equation of a horizontal line given a point, identify the y-coordinate of the point. This value is the constant y-value in the equation y = b.For instance, if a horizontal line passes through the point (4, 5), the equation of the line is y = 5.
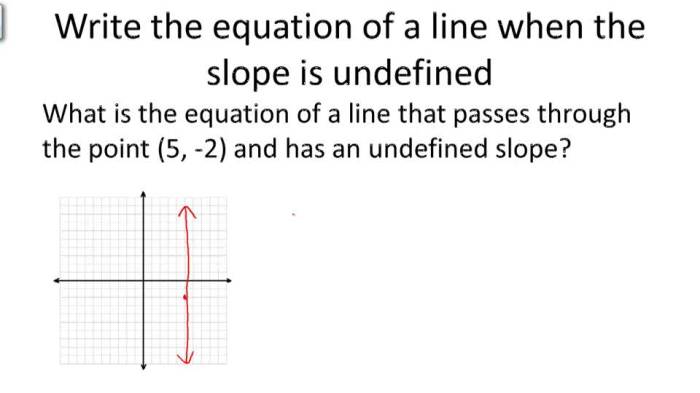
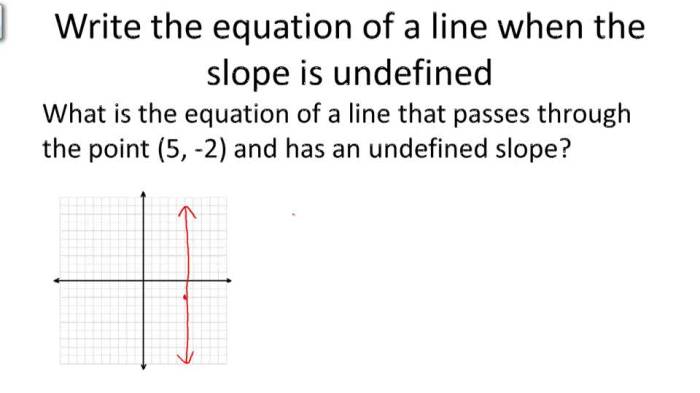
Vertical Lines
Vertical lines, in contrast to horizontal lines, have a constant x-value for all y-values. Crucially, the slope of a vertical line is undefined.
The equation of a vertical line is x = a, where a is the x-intercept.
Consider the line x = 2. This is a vertical line passing through the point (2, 0). Similarly, x = -5 is a vertical line passing through the point (-5, 0).To determine the equation of a vertical line given a point, identify the x-coordinate of the point. This value is the constant x-value in the equation x = a.For example, if a vertical line passes through the point (7, -1), the equation of the line is x = 7.
Closure
In conclusion, mastering the equation of a line empowers you to analyze and model linear relationships. We’ve covered various scenarios, from basic calculations to more intricate situations involving parallel and perpendicular lines. By understanding the different forms of linear equations and their applications, you’ll be equipped to solve a wide range of problems in diverse fields. Hopefully, this comprehensive guide has clarified the concept and given you a solid foundation in finding the equation of a line.